Procesamiento de imágenes digitales con MATLAB
1. Procesamiento digital de imágenes
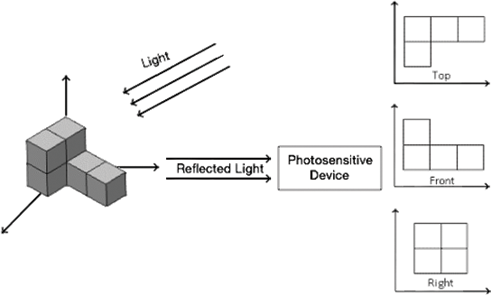
La imagen se puede definir como una información visual bidimensional que se almacena y muestra. Una imagen es creada por dispositivos fotosensibles que capturan la luz de reflexión de la superficie bidimensional del objeto en el mundo real tridimensional (Figura 1). Cada imagen tiene un valor de intensidad o gris en el plano de coordenadas x – y. Si son cantidades finitas y discretas, la imagen se llama imagen digital. En la Figura 2, se muestran algunas imágenes digitales.
El procesamiento digital de imágenes (DIP) tiene las diferentes técnicas para el procesamiento de imágenes digitales. DIP ha estado aplicando muchos campos con avances tecnológicos, como Medicina, Tecnologías de la Información Geográfica, Ciencias Espaciales, Aplicaciones Militares, Seguridad, Aplicaciones Industriales.
1.1. Píxel
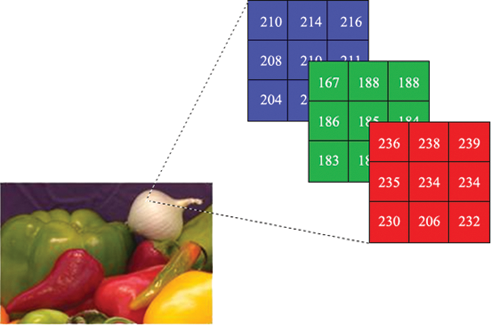
Los píxeles, que se llaman elementos de pel o imagen, se pueden definir como el elemento direccionable más pequeño de la imagen digital. Los píxeles de una imagen en color tienen valores de gris rojo, verde y azul (Figura 3).

1.1.1. Relaciones de píxeles
1.1.1.1. Vecinos de un píxel
Un píxel tiene tres tipos de vecinos diferentes que son 4, 8 y diagonales. Como se muestra en la Tabla 1, el vecino de un píxel (p) en el punto x, y de la imagen (f) se define en esos 4 vecinos;
| f(x – 1, y – 1) | f(x – 1, y) | f(x – 1, y + 1) |
| f(x, y – 1) | fósforo | f(x, y + 1) |
| f(x + 1, y – 1) | f(x + 1, y) | f(x + 1, y + 1) |
Tabla 1.
Vecino de un píxel.
N4(p) se muestra como 4 vecinos de píxel. Cualquier píxel p de la imagen tiene dos vecinos verticales y horizontales, y cada uno de ellos es una distancia unitaria de p, dada porN4(p) = {f(x, y − 1), f(x − 1, y), f(x, y + 1), f(x + 1, y)}N4(fósforo) = {grado Fahrenheit(x, y − 1), grado Fahrenheit(x − 1, y), grado Fahrenheit(x, y + 1), grado Fahrenheit(x + 1, y)}E101
Vecinos diagonales;
Aunque los vecinos diagonales son los mismos que los de 4 vecinos, los píxeles vecinos son la esquina de los píxeles (p) y cada uno de ellos está a una distancia euclidiana de p, dada porND(p) = {f(x − 1, y − 1), f(x − 1, y + 1), f(x + 1, y + 1), f(x + 1, y − 1)}ND(fósforo) = {grado Fahrenheit(x − 1, y − 1), grado Fahrenheit(x − 1, y + 1), grado Fahrenheit(x + 1, y + 1), grado Fahrenheit(x + 1, y − 1)}E1102
8 vecinos;
8-vecinos es una combinación de N4(p) y ND(p) y se muestra como N8(p).N8(p) = {f(x − 1, y − 1), f(x − 1, y + 1), f(x + 1, y + 1), f(x + 1, y − 1), f(x, y − 1), f(x − 1, y), f(x, y + 1), f(x + 1, y)}N8(fósforo) = {grado Fahrenheit(x − 1, y − 1), grado Fahrenheit(x − 1, y + 1), grado Fahrenheit(x + 1, y + 1), grado Fahrenheit(x + 1, y − 1), grado Fahrenheit(x, y − 1), grado Fahrenheit(x − 1,y), grado Fahrenheit(x, y + 1), grado Fahrenheit(x + 1, y)}E103
1.1.1.2. Adyacencia
Si dos píxeles son vecinos y sus valores de nivel de gris satisfacen algún criterio especificado, entonces están conectados. Se utiliza un conjunto de valores de intensidad (V) para definir la adyacencia y la conectividad. Hay tres tipos de adyacencia (Figura 4).
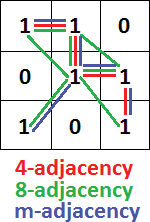
4 adyacencia
Los píxeles p y q tienen 4 adyacencias si son N4(p) con valores de V.
8 adyacencia
Los píxeles p y q tienen 8 adyacencia si son N8(p) con valores de V.
m-adyacencia (mixto)
Los píxeles p y q son m-adyacencia si;
- q está en N4(p) o,
- q está en ND(p) y,
- N4(p) ?? N4(q) = ?? con valores de V.
1.1.1.3. Camino
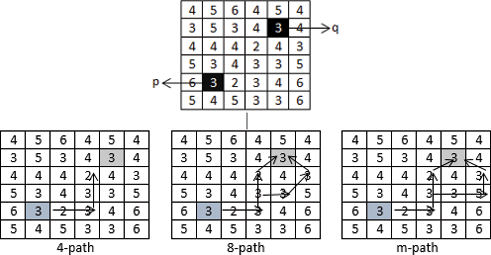
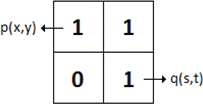
Una ruta desde píxel p con coordenadas (x, y) hasta píxel q con coordenadas (s, t) con valores de V se define como 4‐ ,8‐ o m‐paths dependiendo del tipo de adyacencia especificada.
Según V = {2,3,5}, si queremos encontrar píxeles p y q de 4-, 8- y m‐path, (Figura 5)
1.1.1.4. Medidas de distancia de píxeles
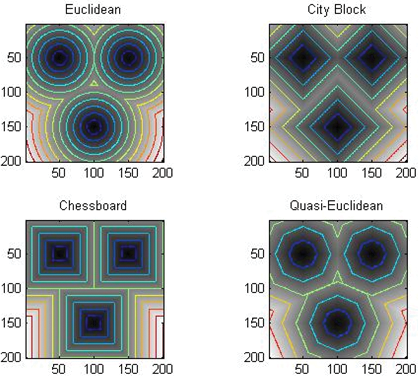
- Distancia euclidiana (De)Deste(p,q)=(x−s)2+(y−t)2??????????????????????????????????√Deste(fósforo,q)=(x−S)2+(y−desoxitimidina monofosfato)2E104
- Distancia de bloque de ciudad (D4)D4(p,q)=|x−s|+∣∣Y−t∣∣D4(fósforo,q)=|x−S|+|y−desoxitimidina monofosfato|E1
- Distancia del tablero de ajedrez (D8)D8(p,q)=max(|x−s|,∣∣Y−t∣∣)D8(fósforo,q)=Max(|x−S|,|y−desoxitimidina monofosfato|)E10000
- Distancia Dm; se define como el camino m más corto.
Según V = {2,3,5}, si queremos encontrar una distancia Dm desde p píxel hasta q píxel (Figuras 6, 7, 8);
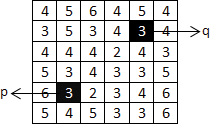
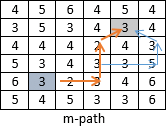
Dm es 5 porque el camino naranja es más corto que el camino azul.

1.2. Resolución espacial
La resolución espacial se puede definir como el número de píxeles por pulgada. En la Figura 10 se muestran diferentes resoluciones espaciales de la misma imagen. La resolución espacial tiene diferentes métodos de medición para diferentes dispositivos.

1.2.1. Puntos por pulgada (DPI)
El DPI se utiliza generalmente en monitores. A veces se llama PPI (Pixeles por pulgada). Pero las dos expresiones tienen una diferencia. El DPI también se utiliza para medir la resolución espacial de las impresoras. Significa que DPI define cuántos puntos de tinta en la imagen impresa por pulgada.
1.2.2. Píxeles por pulgada (PPI)
El IBP se usa generalmente en tabletas, teléfonos móviles, etc. Si a y b son resoluciones de altura y ancho de la imagen, podemos calcular el valor ppi de cualquier dispositivo usando la ecuación 1.PPI=adenina2+vitamina B2√Diagonal S.ize de DispositivosPPyo=adenina2+vitamina B2DyoadeninagigabyteOnewtonadeninaL S.yozeste Ogrado Fahrenheit Destev.yocarbonoesteSE1
Por ejemplo; 1080 × 1920 píxeles, valor de PPI Iphone 6s Plus de 5,5 pulgadas;PPI=10802+19202√5,5≈401 (en se muestra en la aplicacióne web site)PPyo=10802+192025,5≈401 (yodesoxitimidina monofosfato yoS SentalpíaOWnewton yonewton adeninafósforofósforoLeste Westevitamina B Syodesoxitimidina monofosfatoeste)E10000
1.2.3. Líneas por pulgada (LPI)
LPI se refiere a líneas de puntos por pulgada de impresoras. La impresora tiene diferentes valores de LPI como se muestra en las Tablas 2.
| Impresora | Valor de LPI |
|---|---|
| Serigrafía | 45-65 LPI |
| Impresión láser (300 ppp) | 65 LPI |
| Impresión láser (600 ppp) | 85-105 LPI |
Tabla 2.
Valor LPI de la impresora.
1.3. Formatos de archivo de imagen
Los formatos de archivo de imagen son importantes para imprimir, escanear, usar en Internet, etc. Los diferentes formatos se utilizan en el mundo. Los formatos más comunes son jpg, tif, png y gif (Figuras 11). En esta sección, se explican los formatos de archivo más comunes (JPG, TIF, PNG y GIF).

1.3.1. JPG (Grupo Conjunto de Expertos Fotográficos)
JPEG o JPG es el estándar más común para comprimir imágenes digitales. Se utiliza en páginas web, documentos, correo electrónico, etc. Porque las imágenes digitales tienen un tamaño más pequeño que otros formatos de archivo. Sin embargo, las imágenes JPEG tienen una resolución muy baja.
1.3.2. TIF (Formato de archivo de imagen etiquetado)
TIFF o TIF tienen la mejor resolución para usar obras comerciales. Aunque es de muy alta calidad, los archivos tienen un tamaño muy grande.
1.3.3. GIF (formato de intercambio gráfico)
GIF, que se utilizó vídeo de 8 bits para las personas que se conectaban a Internet mediante módem de acceso telefónico, fue diseñado por CompuServe.
1.3.4. PNG (Gráficos de red portátiles)
El formato de archivo PNG tiene un tamaño más pequeño que TIF y más resolución que GIF y JPG. Hoy en día, se utiliza en las páginas web debido a que tiene propiedades de transparencia.Beneficios para la salud de reducir la contaminación del aire¿Pueden disminuir las tasas de mortalidad y las enfermedades cardíacas solo una semana después de que comience la prohibición de fumar en interiores?
2. Procesamiento básico de imágenes con MATLAB
MATLAB es un software muy simple para codificar. Todas las variables de datos en MATLAB se piensan en una matriz y se utilizan operaciones de matriz para analizarlas. MATLAB tiene las diferentes cajas de herramientas según las áreas de aplicación. En esta sección, se presenta MATLAB Image Processing Toolbox y se explica el uso de sus funciones básicas para la imagen digital.
2.1. Leer, escribir y mostrar la imagen
La función imread() se utiliza para leer la imagen. Si ejecutamos esta función con los datos requeridos, la imagen se convierte en una matriz bidimensional (la imagen gris es bidimensional, pero la imagen en color es tridimensional) con filas y columnas que incluyen el valor gris en cada celda.
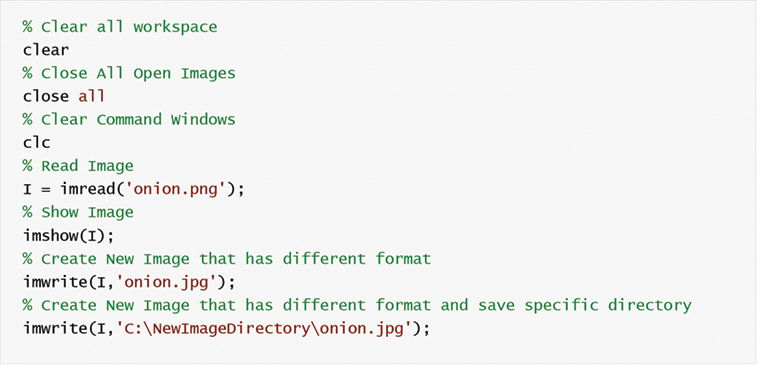
I = imread(‘ruta/nombre de archivo.fileextensión’);
La función imread() solo necesita un archivo de imagen. Si el resultado de la función imread() es igual a una variable, se crea una variable matriz (I). El nombre de archivo, la extensión y la ruta del directorio que contiene la imagen deben escribirse entre dos comillas individuales. Si el script y el archivo de imagen están en la misma carpeta, la ruta no es necesaria.
La variable matriz de la imagen se muestra utilizando la función imshow(). Si muchas imágenes se muestran con secuencia en las diferentes ventanas de figuras, utilizamos la función “figura” para abrir una nueva ventana.
La función imwrite() se utiliza para crear una imagen. Esta función solo requiere un nuevo nombre de archivo de imagen con extensión. Si la nueva imagen se guarda en un directorio específico, la ruta del directorio es necesaria.
2.2. Imagen inversa
Técnica de reserva de imágenes, cada uno de los elementos de la matriz se reemplaza para que sean los elementos de la fila superior a la fila inferior y los elementos de la fila inferior a la fila superior. En otras palabras, la imagen gira sobre el eje vertical.
MATLAB Image Processing Toolbox no tiene función para ello. O bien el script está escrito o se puede usar la función flipdim (Figura 12).


2.3. Reflejo de imágenes
La técnica de duplicación es la rotación de la imagen invertida en el eje horizontal. En MATLAB Image Processing Toolbox tiene la función imrotate() para rotar la imagen. Esta función necesita tres propiedades que son variable de matriz de imagen, ángulo de rotación y método de interpolación (Figura 13).

I_rotate = imrotate(Variable de matriz de imágenes, ángulo, método de interpolación)
Método de interpolación
- “más cercano”: Interpolación del vecino más cercano
- ‘bilineal’: Interpolación bilineal
- ‘bicubic»: Interpolación bicúbica
Ejemplo

2.4. Cambio de imagen
A veces, se puede querer que una imagen cambie hasta cierto valor de píxel en el eje horizontal y vertical. La función imtranslate() se utiliza para desplazar una imagen. En la Figura 14, la imagen cambia 15 px a la derecha y 25 px abajo.


2.5. Cambiar el tamaño de la imagen
Si una imagen se muestra en tamaño grande o pequeño para mostrar detalles o vista general, se debe cambiar su resolución. Estas situaciones se llaman zoom-in y zoom-out. Las cámaras digitales o los dispositivos fotosensibles utilizan lentes ópticas para hacer zoom y alejar. Pero los métodos de interpolación solo se utilizan para imágenes digitales. El problema más común de los métodos de interpolación es el cambio de calidad de imagen (Figuras 15, 16).
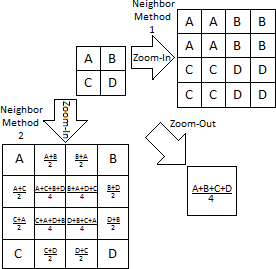
I_resize = imresize(I, Tasa de cambio de tamaño, Método de interpolación)
I es una variable de imagen, si la tasa de cambio de tamaño es mayor que 1, significa zoom-in, de lo contrario zoom-out.


3. Mejora de la imagen
En algunos casos, una imagen tiene información inútil o insuficiente para extraer objetos debido a diferentes defectos. Por lo tanto, la imagen debe procesarse utilizando diferentes técnicas de procesamiento de imágenes digitales para eliminar los defectos o artefactos. En esta sección, se explican algunos métodos principales para aumentar la visibilidad y disminuir los defectos.
3.1. Brillo
El brillo de una imagen se ajusta sumando o restando un cierto valor al nivel de gris de cada píxel.G(i, j)= F(i, j)+b b>0 Br.ightness incerfacilidadb<0 Br.ightness decrfacilidadG(yo,J)= F(yo,J)+vitamina B vitamina B>0 BRyogigabyteentalpíadesoxitimidina monofosfatonewtonesteSS yonewtoncarbonoesteResteadeninaSestevitamina B<0 BRyogigabyteentalpíadesoxitimidina monofosfatonewtonesteSS DestecarbonoResteadeninaSesteE10000
I_adjust = imadjust(I, [low_in; hig_in], [low_out;high_out])
Los nuevos valores de intensidad de imagen (I_adjust) están entre los valores de gris low_out y high_out (Figura 17).




El script MATLAB anterior se utiliza para la imagen gris, pero queremos cambiar el brillo de la imagen en color, por lo que debemos cambiar todos los valores de intensidad del canal R (rojo), G (verde) y B (azul) de la imagen (Figura 18).
3.2. Contraste
El contraste de una imagen se puede cambiar multiplicando todo el valor gris de píxeles por un cierto valor.G(i, j)=c*F(i, j) c>0 cont.Rast incrfacilidadc<0 contRast DecrfacilidadG(yo,J)=carbono*F(yo,J) carbono>0 carbonoOnewtondesoxitimidina monofosfatoRadeninaSdesoxitimidina monofosfato yonewtoncarbonoResteadeninaSestecarbono<0 carbonoOnewtondesoxitimidina monofosfatoRadeninaSdesoxitimidina monofosfato DestecarbonoResteadeninaSesteE10000
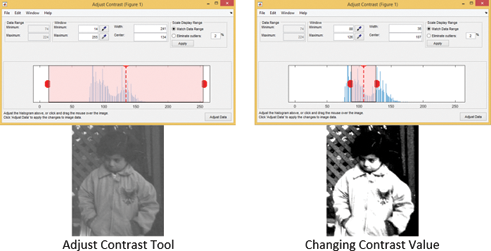
MATLAB Image Processing Toolbox tiene la herramienta Contrast Adjust para cambiar el contraste de una imagen. Como se muestra en la Figura 19, la interfaz gráfica de usuario permite al usuario cambiar el contraste mediante el manejo.

3.3. Negativo
Los valores de intensidad de la imagen se invierten como lineales para la imagen negativa (Figura 20).


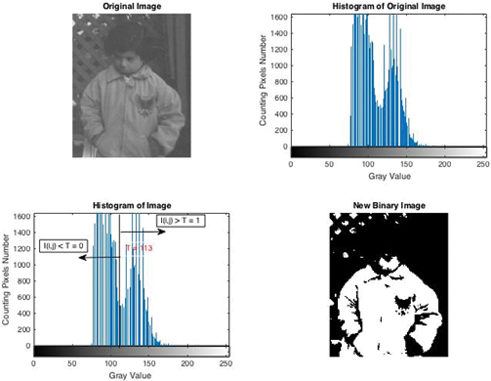
3.4. Umbral
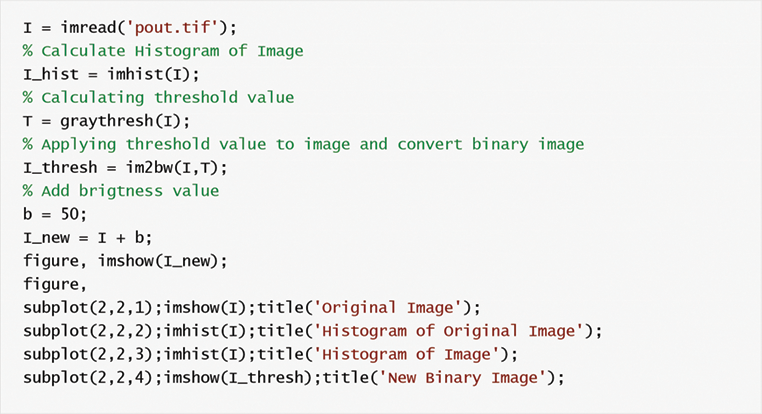
El umbral se utiliza generalmente para convertir la imagen a una imagen binaria (valor gris y 1). El algoritmo de umbralización se define en la ecuación 2.G (x),y)={yo(x,y)≥T 1yo(x, y)<T 0G(x,y)={yo(x,y)≥T 1yo(x,y)<T 0E2
I es la imagen original, x e y son números de fila y columna, T es valor umbral, G es nueva imagen fter aplicando umbral (Figura 21).
| Valor gris | Conteo del número de píxeles |
|---|---|
| 75 | 2 |
| 76 | 38 |
| 77 | 0 |
| 78 | 389 |
| 79 | 1245 |
| 80 | 0 |
| 81 | 1518 |
Tabla 3.
Histograma de valores grises específicos.
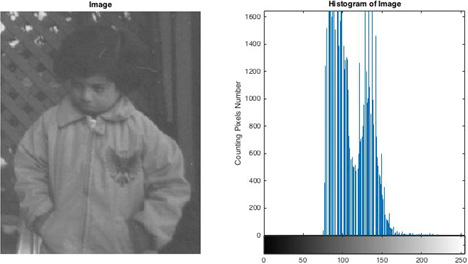
3.5. Histograma
El histograma cuenta el número de valores grises de los píxeles en las imágenes. Cada píxel de la imagen tiene un valor de gris entre 0 y 255. Como se muestra en la Tabla 3, contar píxeles nos da información sobre la imagen u objetos de la imagen. El histograma de la imagen se muestra en la Figura 22.
El histograma de la imagen se calcula utilizando la función imhist(image) en MATLAB.

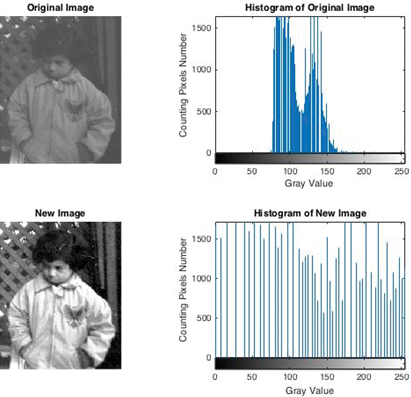
3.6. Ecualización del histograma
La ecualización del histograma se define como una técnica para ajustar el contraste de una imagen utilizando todos los valores de gris para ecualizar tanto como sea posible. Algunas situaciones funcionan bien y la imagen se muestra muy bien; a veces, no es buena y la nueva imagen es más oscura que la imagen original (Figura 24).
| 1 | 1 | 1 | 1 | 1 |
| 3 | 3 | 0 | 0 | 2 |
| 3 | 3 | 2 | 2 | 2 |
| 6 | 4 | 4 | 2 | 6 |
| 6 | 7 | 7 | 5 | 5 |
Tabla 4.
Valores grises de píxeles de imagen.
Explicamos la ecualización del histograma con un examen. Piensas en una imagen, y su mapeo de intensidad se muestra a continuación. Hay ocho niveles de grises posibles de 0 a 7. Si aplicamos la ecualización del histograma a los valores grises de píxeles de la imagen que se muestran en la Tabla 4, ¿qué nuevo histograma de imagen será?
Paso 1: Buscar el histograma de la imagen (Tabla 5)
| yo | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| f(I) | 2 | 5 | 5 | 4 | 2 | 2 | 3 | 2 |
Tabla 5.
Histograma.
Paso 2: Calcular la distribución acumulativa de frecuencias (CFD)
| yo | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| f(I) | 2 | 5 | 5 | 4 | 2 | 2 | 3 | 2 |
| CFD | 2 | 2 + 5 = 7 | 7 + 5 = 12 | 12 + 4 = 16 | 16 + 2 = 18 | 18 + 2 = 20 | 20 + 3 = 23 | 23 + 2 = 25 |
Tabla 6.
Calcule el Distrubitón de Frecuencia Acumulada (CFD).
Paso 3: Calcule el nuevo valor gris de píxeles usando la ecuación 3h(v)=fLoor(C.FD(v)−CFDMin(MxN)−CFDMinx(L−1))entalpía(v.)=grado FahrenheitLOOR(C.FD(v.)−C.FDmegabyteyonewton(M.xN)−C.FDmegabyteyonewtonx(L.−1))E3
h es un nuevo valor de gris, v es número de píxel, MxN es valor de fila de imagen y columna, L es nivel de gris (en nuestra imagen L es 8)
Si calculamos el píxel de 4 números;h(4)=fLoor((16−2)/((5×5)−2) x(8−1))≈fLoor(4,26)≈4entalpía(4)=grado FahrenheitLOOR((16−2)/((5×5)−2) x(8−1))≈grado FahrenheitLOOR(4,26)≈4E10000
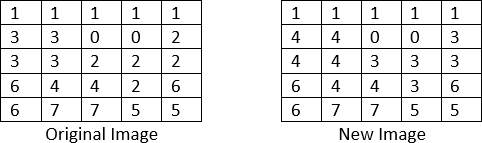
Después de que todos los valores de gris píxel se calculen utilizando la Ecuación 3, los resultados de los nuevos valores de gris serán como en la Tabla 7.
| yo | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| f(I) | 2 | 5 | 5 | 4 | 2 | 2 | 3 | 2 |
| CFD | 2 | 7 | 12 | 16 | 18 | 20 | 23 | 25 |
| entalpía | 0 | 1 | 3 | 4 | 4 | 5 | 6 | 7 |
Tabla 7.
Nuevos valores grises.
Después de aplicar la ecualización del histograma a la imagen, se muestran nuevos valores de gris en la Figura 23.

Matlab Image Processing Toolbox tiene los diferentes tipos de filtros como se muestra en la Tabla 8.
4. Color
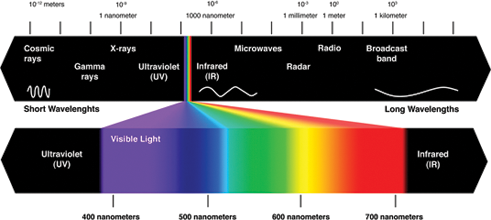
Los humanos tienen muy buenos dispositivos fotosensibles que se llaman ojos. Newton descubrió que la luz tiene un espectro de color diferente que pasa a través del prisma de cristal. Creemos que el ojo humano es un prisma de cristal que se llama lente. El cristalino enfoca la luz hacia la retina de los ojos. De modo que los humanos vean el espectro de color visible de la luz reflejada desde los objetos. El espectro de color se muestra en la Figura 25. El ser humano siente la longitud de onda de la luz entre 400 y 700 nm.
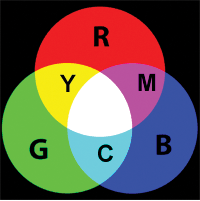
Los ojos ven los colores como una combinación de primarios que son Rojo (R), Verde (G) y Azul (B). Para que todos los colores visibles se produzcan a partir de colores primarios. Los colores secundarios, que se producen con la adición de colores primarios, son Amarillo (Rojo + Verde), Magenta (Rojo + Azul) y Cian (Verde + Azul), como se muestra en la Figura 26.
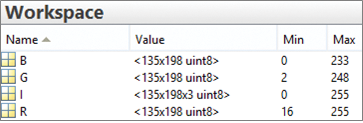
En la caja de herramientas de procesamiento de imágenes MATLAB, una imagen en color tiene datos tridimensionales uint8 (entero sin signo de 8 bits). Cada dimensión corresponde a un canal de color que es rojo, verde o azul. Si queremos, podemos procesar cada canal de color. Como se muestra en la Figura 27, cada canal de color se divide de la imagen.


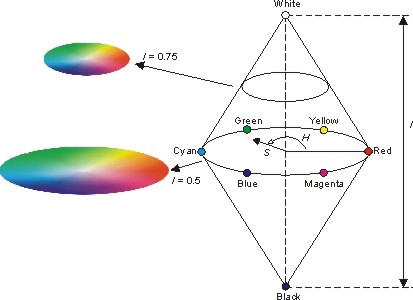
4.1. HSI
Como se muestra en la Figura 29, cada color representa tres componentes como H (Hue), S (Saturación), I (Intensidad). El tono, que se puede definir como tasa de color puro, es una forma de ángulo entre 0° y 360°. Rojo, verde, azul son 0°, 120° y 360°, y Amarillo, Cian y Magenta son 60°, 180°, 300°. La saturación, que muestra cómo el color debe ser puro, toma valor entre [0, 1]. La intensidad son las dimensiones de la luminosidad o la oscuridad. El rango de intensidad está entre 0 (negro) y 1 (blanco).

MATLAB usa rgb2hsv(imagen) o escribe script usando Eqs. (4)–(6) para convertir la imagen en color a componentes HSI. Si queremos convertir de imagen HSI a imagen RGB, utilizamos hsv2rgb (imagen HSI).H={θ360−θ si B≤Gsi B>G inteligenciah θ= coS−1{12[(R−G)+(R−B)][(R-G)2+(R−B)(G−B)]12/}H={θ360−θ yogrado Fahrenheit B≤Gyogrado Fahrenheit B>G Wyodesoxitimidina monofosfatoentalpía θ= carbonoOS−1{12[(R−G)+(R−B)][(R−G)2+(R−B)(G−B)]12}E4S.=1−3(R+G+B)[min(R,G,B)]S.=1−3(R+G+B)[megabyteyonewton(R,G,B)]E5yo=13[R+G+B]yo=13[R+G+B]E6

4.2. YIQ
YIQ, que es definido por el Comité Nacional del Sistema de Televisión (NTSC), produce la luminancia y la crominancia. Utilizamos la ecuación 7 para producir componentes YIQ a partir de imágenes RGB (Figura 31), y la ecuación 8 se utiliza para convertir de YIQ a RGB.??????????YyoQ??????????=??????????0,2990,5960,2110,587−0,0274−0,5230,114−0,3220,311????????????????????RGB??????????[YyoQ]=[0,2990,5870,1140,596−0,0274−0,3220,211−0,5230,311][RGB]E7??????????RGB??????????=??????????1110,986−0,0272−1,1060,621-0,6491,703????????????????????YyoQ??????????[RGB]=[10,9860,6211−0,0272−0,6491−1.1061,703][YyoQ]E8


4.3. Imagen gris
La imagen gris se produce utilizando la ecuación 9 según los estándares NTSC. Sin embargo, podemos calcular diferentes métodos, pero MATLAB utiliza estándares NTSC y tiene función rgb2gray (imagen RGB) (Figura 32).GI=0,299R+0,587G+0,114BGyo=0,299R+0,587G+0,114BE9
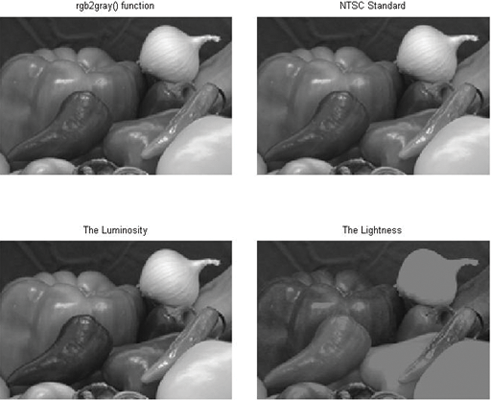
Otros métodos;
- El promedio; GI = 0.33R + 0.33G + 0.33B
- La ligereza; GI = (max(R,G,B) + (min(R,G,B))/2
- La luminosidad; GI = 0,21R + 0,72G + 0,07B

5. Operaciones morfológicas
MATLAB Image Processing Toolbox solo utiliza imágenes binarias para operaciones morfológicas como abrir, cerrar, etc.
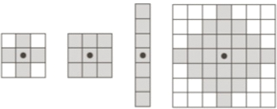
5.1. Elemento estructurante
El elemento estructurante (SE) es una forma que tiene diferentes tamaños (3 × 3, 4 × 4, 5 × 5, etc.) y formas (Figura 33). SE se aplica a una imagen para obtener resultados de dibujo sobre cómo cambian los objetos en la imagen (Figura 34). SE se utiliza generalmente para operaciones de dilatación, erosión, apertura y cierre.
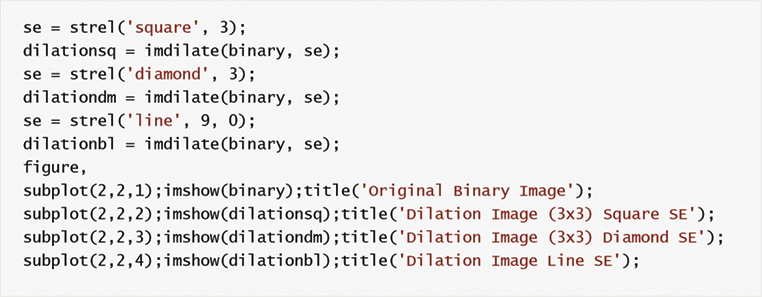
5.2. Dilatación
La dilatación es un procesamiento morfológico para hacer crecer un objeto en la imagen binaria. Se muestra con ⊕ imagen (Figura 35).C.=A BC.=ABE10000
C es la nueva imagen, A es la imagen original y B es el elemento estructurante.

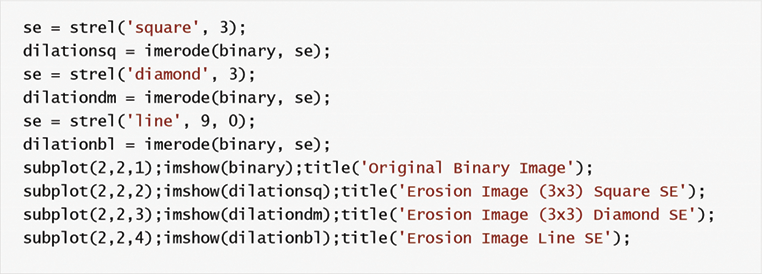
5.3. Erosión
La erosión es el otro operador morfológico de una imagen binaria para usar la erosión de los píxeles de los objetos de la imagen. Se muestra como símbolo ⊖.C.=A⊖BC.=A⊖BE10000

5.4. Apertura y cierre
Como se muestra en (Figura 36), la apertura y el cierre son la combinación de operadores de erosión y dilatación, como se muestra en las ecuaciones 10 y 11.C.=(A B)⊕BC.=(AB)⊕BE10C.=(A⊕B) BC.=(A⊕B)BE11


5.5. Convolución
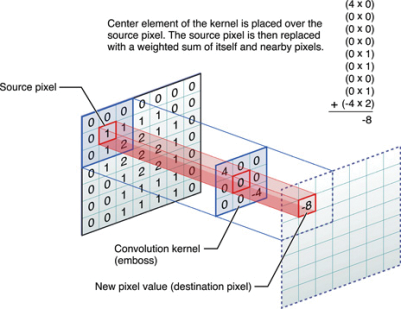
La convolución se utiliza generalmente para modificar la característica espacial de una imagen (Figura 38). En la convolución, un nuevo valor gris de píxel se encuentra por los píxeles promedio ponderados que son vecinos de ella. El valor gris de los píxeles vecinos está ponderado por un coeficiente de matriz que se llama núcleo de convolución. Según las aplicaciones, la matriz del núcleo tiene diferentes tamaños, como 3 × 3, 5 × 5, 7 × 7 (Figura 37).
La definición matemática de la convolución se muestra en la ecuación 12;G (x), y)=∑newtonJ=−n∑megabytei=−mK(i, j)F(x−i,y−j)=k*FG(x,y)=∑J=−newtonnewton∑yo=−megabytemegabyteK(yo,J)F(x−yo,y−J)=K*FE12
k: matriz del núcleo de convolución
F: procesar la imagen
si w y h son fila y columna de la imagen ⇒(m = (w – 1)/2)|(n = (h – 1)/2)

Matlab Image Processing Toolbox tiene los diferentes tipos de filtros como se muestra en la Tabla 8.
| Valor | Descripción |
|---|---|
| Media | Promedio del filtro |
| disco | Filtro de promedio circular (caja de píldoras) |
| gaussiano | Filtro gaussiano de paso bajo |
| laplaciano | Se aproxima al operador laplaciano bidimensional |
| tronco | Filtro laplaciano de Gaussian |
| movimiento | Aproxima el movimiento lineal de una cámara |
| prewitt | Filtro de énfasis horizontal de bordes Prewitt |
| sobel | Filtro de énfasis horizontal de bordes Sobel |
Tabla 8.
Tipos de filtros de la caja de herramientas de procesamiento de imágenes Matlab.

5.6. Detección de bordes
La detección de bordes se utiliza para encontrar el borde de los objetos en la imagen (Figura 39). Los algoritmos comunes de detección de bordes son Sobel, Canny, Prewitt, Roberts, etc.


5,7. Etiquetado
A los píxeles se les asignan diferentes etiquetas debido a que pertenecen a diferentes regiones (u componentes u objetos). En la Figura 40, los objetos de la imagen tienen los diferentes valores de etiqueta y muestran diferentes colores en MATLAB.

La función [Boundary,Labels] = bwboundaries(binary image, ‘noholes’) utiliza para el etiquetado. En primer lugar, la imagen debe ser una imagen binaria, si no lo es, debe convertirla a una imagen binaria. En segundo lugar, todos los objetos deben ser blancos (1) y el fondo debe ser negro (0) para usar el método de “noholes”. Utilizamos esta función con dos variables. Uno de ellos es la dirección de los píxeles de frontera, y otro son los números de etiqueta y sus direcciones.
6. Ejemplo de aplicación
La última sección de este capítulo es una aplicación de muestra que trata sobre la extracción de algunas características morfológicas de múltiples albaricoques en una imagen digital. En primer lugar, se leen imágenes digitales originales y de fondo (Figuras 41, 42). Después de eso, la imagen original recortada se resta de la imagen de fondo. El proceso de recorte se utiliza para extraer área específica de la imagen original (Figura 42). La imagen restada (Figura 44) se convierte en imagen gris como se muestra en la Figura 45. El proceso de umbral se aplica a la imagen gris para convertir la imagen binaria (Figura 46). A veces, algunos artefactos pueden ocurrir en imágenes binarias. Antes del etiquetado, se eliminan los grupos de píxeles de conexión que son menores que el valor específico (menores de 50 px en esta aplicación) (Figura 47). Después del etiquetado (Figura 48), podemos encontrar todas las características morfológicas de los objetos como se muestra en la Figura 49.














